「DL」 GAN 的数学原理
分布的相似性
两个分布 $P, Q$,$x = { x_1, x_2, \cdots, x_m}$ 为分布 $Q$ 下的样本;
\(\begin{align}
l(\theta) &= \prod_{i=1}^m P(x_i;\theta) \label{Likelihood}\\
D_{\mathrm {KL}}(P\|Q) &= \int P(x)\ln {\frac{P(x)}{Q(x)}} dx \label{kl_divergence}
\end{align}\)
公式 $\eqref{Likelihood}$ 为似然函数,公式 $\eqref{kl_divergence}$ 为 KL 散度;二者关系如下:
\(\begin{align}
\theta^* = \arg \max_\theta \prod_{i=1}^m P(x_i;\theta) = \arg \min_\theta D_{\mathrm {KL}}(Q\|P)
\end{align}\)
以下是推导过程:
\(\begin{align}
\theta^* &= \arg \max_\theta l(\theta) \\
&= \arg \max_\theta \prod_{i=1}^m P(x_i;\theta) \\
&= \arg \max_\theta \log \prod_{i=1}^m P(x_i;\theta) \\
&= \arg \max_\theta \sum_{i=1}^m \log P(x_i;\theta) \\
&= \arg \max_\theta \frac{1}{m} \sum_{i=1}^m \log P(x_i;\theta) \\
&= \arg \max_\theta \mathbb E_{x \sim Q} \log P(x;\theta) \\
&= \arg \max_\theta \int Q(x) \log P(x;\theta) dx \\
&= \arg \max_\theta \int Q(x) \log P(x;\theta) dx - \int Q(x) \log Q(x) dx\\
&= \arg \max_\theta \left(\int Q(x) \log P(x;\theta) - \int Q(x) \log Q(x)) dx \right)\\
&= \arg \max_\theta \int Q(x) \left(\log P(x;\theta) - \log Q(x) \right) dx\\
&= \arg \max_\theta \int Q(x) \left(\log \frac{P(x;\theta)}{Q(x)} \right) dx\\
&= \arg \min_\theta \int Q(x) \left(\log \frac{Q(x)}{P(x;\theta)} \right) dx\\
&= \arg \min_\theta D_{\mathrm {KL}}(Q\|P)
\end{align}\)
损失函数
GAN 的 loss 函数等于 JS 散度的推导;
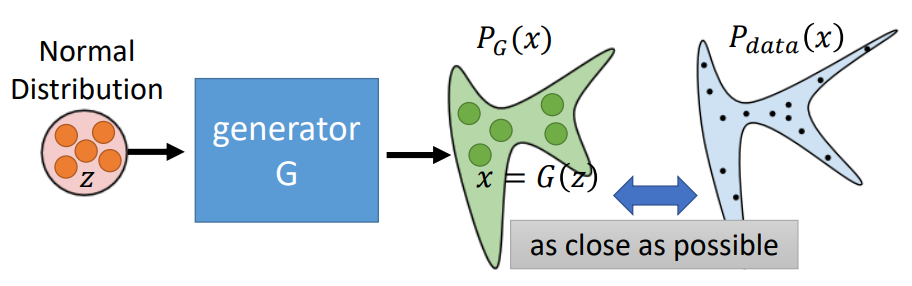
图1:生成器流程示意图[^1]
从理论上来看,GAN 的最终目标是要得到最优的生成器 $G^*$ 和 判别器 $D^*$:
\(\begin{align}
G^* &= \arg \min_G Div(P_G, P_{data}) \\
D^* &= \arg \max_D Div(P_G, P_{data}) \\
\end{align}\)
对于判别器 $D$ 来说就是一个二分类问题; 区分真实样本还是生成样本,那么从数学角度看:
\(\begin{align}
V(G, D) &= \mathbb E_{x \sim P_{data}}[\log D(x)] + \mathbb E_{x \sim P_G}[\log (1-D(x)] \label{loss_gan} \\
&= \int_x P_{data}(x)\log D(x) dx + \int_x P_G(x) \log (1-D(x)) dx \\
&= \int_x [P_{data}(x)\log D(x) + P_G(x) \log (1-D(x))] dx \\
\end{align}\)
上式假设 $D$ 可以是任意函数
\(\begin{align}
f(D) &= a \log(D) + b \log(1-D) \\
\frac{df(D)}{dD} &= a \times \frac{1}{D} + b \times \frac{1}{1-D} \times (-1) = 0 \\
&\Rightarrow a \times \frac{1}{D^*} = b \times \frac{1}{1-D^*} \\
&\Rightarrow a \times (1-D^*) = b \times D^* \\
&\Rightarrow D^* = \frac{a}{a+b} \\
\end{align}\)
二阶导数小于0,所以函数是凸函数,具有极大值;
\(\begin{align} D^* &= \arg \max_D V(G, D) \\ &= \frac{P_{data}(x)}{P_{data}(x) + P_G(x)} \\ V(G, D*) &= \int_x P_{data}(x)\log \frac{P_{data}(x)}{P_{data}(x) + P_G(x)} dx \\ &+ \int_x P_G(x) \log \left(1-\frac{P_{data}(x)}{P_{data}(x) + P_G(x)}\right) dx \notag\\ &= \int_x P_{data}(x)\log \frac{P_{data}(x)}{P_{data}(x) + P_G(x)} dx \\ &+ \int_x P_G(x) \log \frac{P_G(x)}{P_{data}(x) + P_G(x)} dx \notag\\ &= \log\frac{1}{2} + \int_x P_{data}(x)\log \frac{P_{data}(x)}{(P_{data}(x) + P_G(x))/2} dx \\ &+ \log\frac{1}{2} + \int_x P_G(x) \log (\frac{P_G(x)}{(P_{data}(x) + P_G(x))/2}) dx \notag\\ &= -2\log2 + KL\left(P_{data}\|\frac{P_{data}+P_G}{2} \right) + KL\left(P_G\|\frac{P_{data}+P_G}{2} \right) \\ &= -2\log2 + 2JS(P_{data}\|P_G) \end{align}\) 结论: $V(G, D*)$ 就是 $P_{data}$ $P_G$ 的 JS 散度;
生成器要在当前状态下(判别器使得 $V(G, D*)$ 最大的情况下)使 $V(G, D)$ 最小:
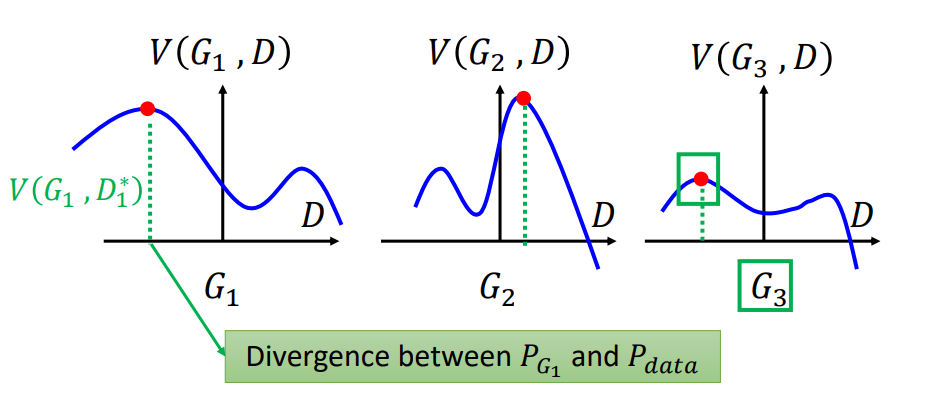
图2:min max示意图[^1]
\(\begin{align} G^* &= \arg \min_G \max_D V(G, D) \label{loss_generator} \\ \end{align}\)
训练过程:
- 固定 $G$,训练 $D$,正样本来自训练集,负样本来自生成器;
- 固定 $D$,训练 $G$;
data 的积分去哪了
为什么要做 JS 散度的推理
Loss 用的什么
- :o: GAN 训练过程中,真实样本和生成样本分别作用于哪些网络
Comments