「DL」 生成模型简介
生成模型即能够产生同类型新数据的模型;可以根据输入产生我们所期望的输出;
大家对于 DL 的认识
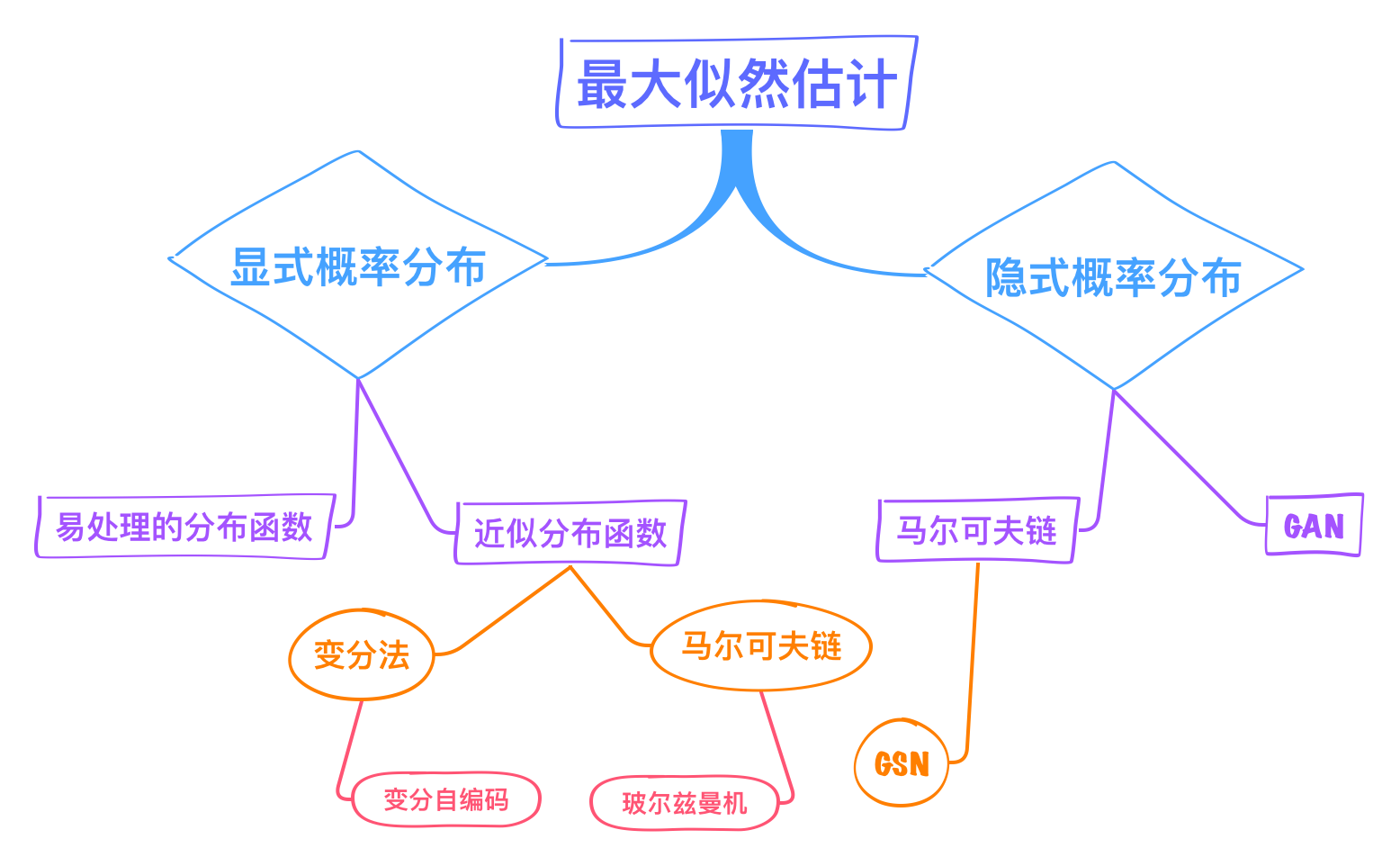
图1:基于最大似然估计的生成模型分类 :ghost:
典型的应用有超分辨率、图文互转、艺术创作等;
1 自回归模型
:ghost: 自回归模型通过对图像数据的概率分布 $p_{data}(x)$ 进行显式建模,从而定义一个易处理的密度函数,然后利用最大似然估计优化模型:
\begin{equation}
p_{data}(x)=\prod_{i=1}^n p(x_i|x_1,x_2,…,x_{i-1})
\end{equation}
给定 $x_1,x_2,…,x_{i-1}$ 条件下,所有 $p(x_i)$ 的概率乘起来就是图像数据的分布;如果使用 RNN 对上述依然关系建模,就是 pixelRNN;如果使用 CNN,则是 pixelCNN;由于两者都是逐像素操作,所以速度很慢;语音领域大火的 WaveNet 就是一个典型的自回归模型;
2 自编码
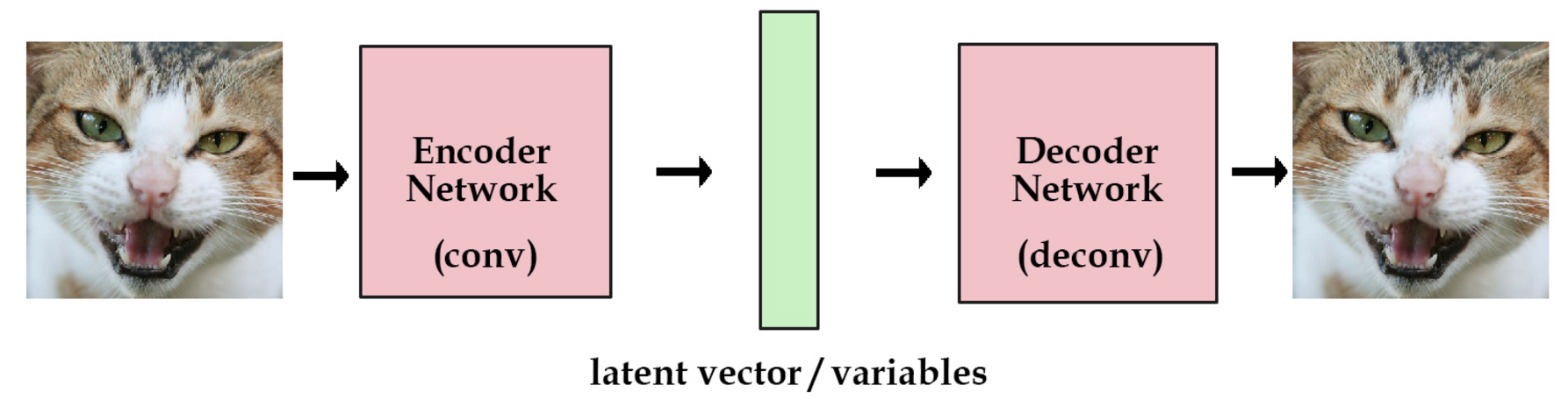
图2:自编码网络示意图
自编码网络最初是为了做数据压缩;因为要做训练,所以包含编码器和解码器两部分;后来解码器被单独拿出来作为生成器;
缺点是模型受训练数据限制太重,泛化能力并不好;于是有了变分自编码;
3 变分自编码器
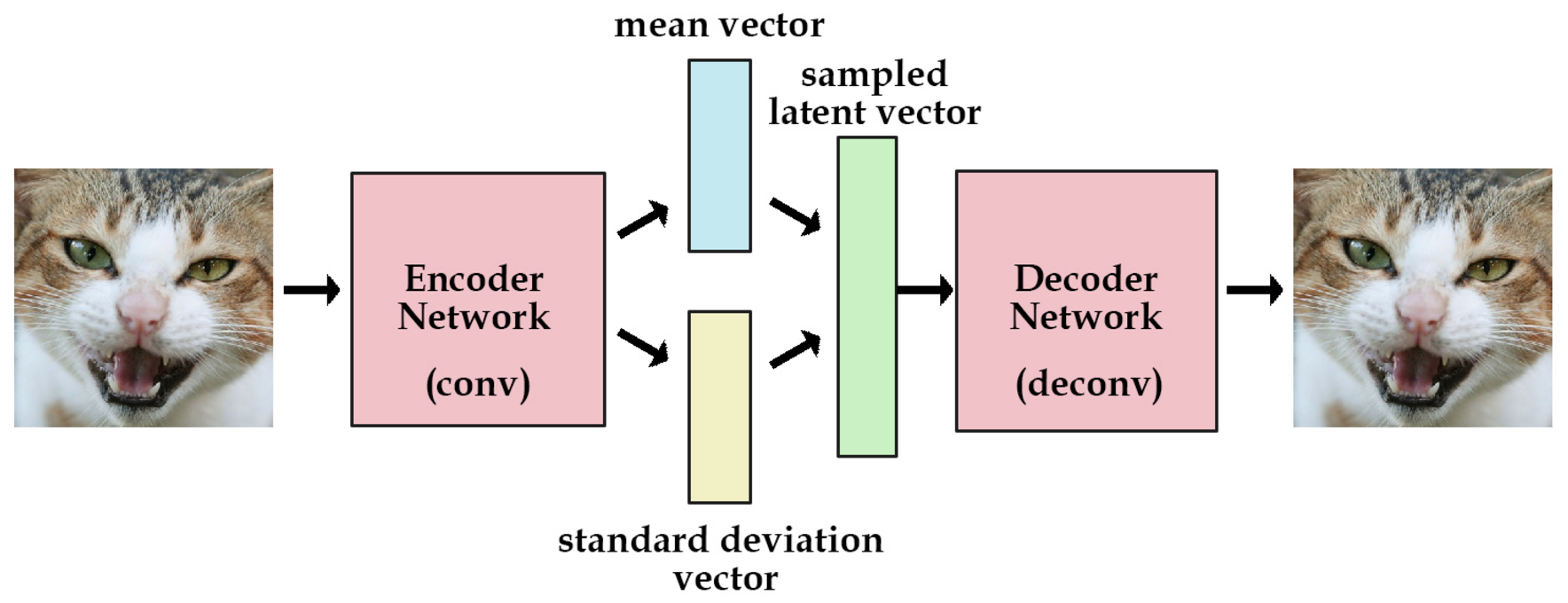
图3:变分自编码网络示意图
VAE,编码器不再直接生成编码,而是假设隐变量服从正态分布,以此增强隐变量的丰富程度;根据训练数据生成均值和方差,再得到编码(隐变量);然后把编码送入解码器进行重构;
VAE 的损失函数包括两部分,重建损失和分布相似度度量,前者用的均方差,后者用的 KL 散度;
VAE 和 GAN 均是学习了隐变量到真实数据分布的映射,但是和 GAN 不同的是:
- GAN 的思路比较粗暴,使用一个判别器去度量分布转换模块(即生成器)生成的数据与真实数据在概率分布上的距离;
- VAE 则没有那么直观,VAE 通过约束隐变量服从标准正态分布以及重构数据实现了分布转换映射;生成的图像比较模糊;
-
:o: 到底是编码器在逼近真实数据分布,还是解码器在逼近
当然是解码器,文中所提的分布指的是隐变量的分布,KL 散度计算的是隐变量和正态分布之间的距离; -
:o: 为什么生成图像比较模糊,数学推导?
:ghost:
4 GAN
发音:gan(轻声),也可以三个字母分开读;
- :o: 如何衡量生成样本的效果
- 具有显式分布的用 KL 散度和 JS 散度等;
- 隐式分布的,针对生成结果做二分类;
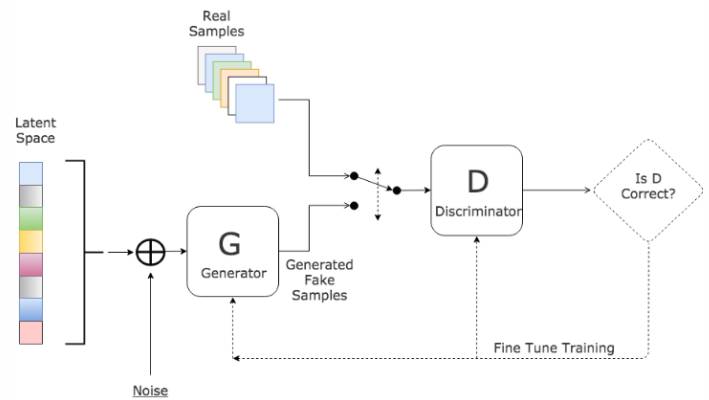
Generative Adversarial Nets,一个通过对抗的方式评估生成模型效果的网络结构,其包含两个结构:
生成器:一个隐式捕获训练集的数据分布,并以此生成新样本的网络;
判别器:一个判断输入的样本是来自训练集还是生成器的网络;
生成器的目标是减小生成样本和训练样本的差距,判别器的目标是增大生成样本和训练样本的差距,由此形成了对抗;
从博弈论角度看是一个「极小化极大博弈」或「零和博弈」;:ghost:
5 生成式模型对比
- 自回归模型通过对概率分布显式建模来生成数据;
- VAE 和 GAN 均是:假设隐变量 $z$ 服从某种分布,并学习一个映射 $X=G(z)$ ,实现隐变量分布 $z$ 与真实数据分布 $p_{data}(x)$ 的转换;
- GAN 使用判别器去度量映射 $X=G(z)$ 的优劣,而 VAE 通过隐变量 $z$ 与标准正态分布的 KL 散度和重构误差去度量;
GAN 生成的样本更丰富,清晰度更高;
End
Comments