「DL」 GAN 预备知识

文章将简略介绍 GAN 中用到的深度学习概念；

1 技能

• 编程语言：python，python 第三方库（numpy，pandas，matplotlib/seaborn）；
• 工具：pip，jupyter，docker（可选）
• 深度学习框架：Tensorflow，MXNet，Pytorch，Keras，Caffe，Caffe2 中的一种；

2 术语

2.1 数学

2.1.1 初等数学

1. 对数
   和差公式：$\log M \cdot N = \log M + \log N$，$\log \frac{M}{N} = \log M - \log N$
   次方公式：$\log_{\alpha^n} x^m = \frac{m}{n} \log_\alpha x$

2.1.2 微积分

1. 运算法则
   $\int [f(x) \pm g(x)] dx = \int f(x) dx \pm \int g(x) dx$

2.1.3 概率论

1. 随机变量
   给定样本空间 $S$，如果其上的实值函数 $X:S$ 是实值可测函数，则称 $X$ 为随机变量；称其为变量是指可作为因变量；
   谁可以作为因变量，函数值还是函数

2. 概率分布
   概率累加所得，故又叫「累积分布函数」；
   设 $P$ 为概率， $X$ 为随机变量，则函数 $F(x) = P(X \leq x) \quad (x\in \mathbb R)$ 称为 $X$ 的概率分布函数；如果将 $X$ 看成是数轴上的随机点的坐标，那么，分布函数 $F(x)$ 就表示 $X$ 落在区间 $(-\infty, x]$ 上的概率；
   $F(x) = P(X \leq x)$ 也会写作 $F_X(x)$

3. 概率密度函数
   为连续随机变量定义的，本身不是概率，在 $x$ 上积分后才是概率：
   对于一维随机变量 $X$，设它的概率分布是 $F_X(x)$，满足：
   $ \forall -\infty <a<\infty ,\quad F_X(a) = \int _{-\infty }^{a} f_X(x)\,dx$
   那么 $f_X(x)$ 是它的概率密度函数；

4. 概率质量函数
   为离散随机变量定义的，等于概率：$p(x) = P(X=x)$

5. 期望
   函数 $f(x)$ 关于概率分布 $P(\mathtt x)$ 的期望（expectation）（即变量 $x$ 由概率分布 $P(x)$ 产生时，$f$ 作用与 $x$ 时，$f(x)$ 的平均值）:
   \(\begin{align} {\mathbb E}_{\mathtt x \sim P}[f(x)] &= \sum_x {P(x)f(x)} \quad \label{EXP_discrete}\\ {\mathbb E}_{\mathtt x \sim p}[f(x)] &= \int {P(x)f(x)dx} \label{EXP_variables} \end{align}\)
   $\eqref{EXP_discrete}$ 是离散型，$\eqref{EXP_variables}$ 是连续型；
   条件明确时，$\mathbb {E}_{\mathtt x \sim P}[f(x)]$ 会简化成 $\mathbb {E}_{\mathtt x}[f(x)]$ 、$\mathbb {E}[f(x)]$ 或 $\mathbb {E}$

6. 高斯分布
   正态分布
   \begin{equation} \mathcal N(x; \mu, \sigma^2) = \sqrt{\frac{1}{2\pi \sigma^2}} \exp \left ( -\frac{1}{2\sigma^2} (x-\mu)^2 \right )
   \end{equation} 常在自然和社会科学中代表一个不明的随机变量¹:
   • 真实情况下许多模型的分布都接近正态分布；中心极限定理说明了很多独立随机变量的和接近正态分布；
   • 具有相同方差的所有可能的概率分布中，正态分布在实数上具有最大的不确定性；也就是说正态分布是对模型加入先验知识最少的分布；
     $N(x; \mu, \sigma^2)$ 在有些文献中也写作 $N(x|\mu, \sigma^2)$

7. 最大似然估计
   利用已知的样本，反推最有可能（最大概率）导致这样结果的参数值（概率分布）；
   对于样本 $D={x_1, x_2, \cdots, x_n}$ 的 $\theta$ 的似然函数为：
   \(\begin{align} l(\theta) &= p(D;\theta) \\ &= p(x_1, x_2, \cdots, x_n;\theta) \\ &= \prod_{i=1}^N p(x_i;\theta) \label{Likelihood} \end{align}\) 为什么 似然计算时要用乘而不是加 最大似然估计：那么就存在一个 $\theta$ 使似然函数 $l(\theta)$ 的值最大：
   \begin{equation} \theta^* = \arg \max_\theta l(\theta) = \arg \max_\theta \prod_{i=1}^N p(x_i;\theta) \end{equation}

8. KL 散度
   相对熵，是两个概率分布 $P$ 和 Q 差异的度量，是非对称的；P 表示数据的真实分布，Q 表示模型分布或 P 的近似分布； \(\begin{align} D_{\mathrm {KL}}(P\|Q) &= \sum_{i}P(i)\ln {\frac {P(i)}{Q(i)}} \label{kl_discrete} \\ D_{\mathrm {KL}}(P\|Q) &= \int_{-\infty }^{\infty} P(x)\ln {\frac {P(x)}{Q(x)}} dx \label{kl_divergence} \end{align}\)
   $\eqref{kl_discrete}$ 是离散型，$\eqref{kl_divergence}$ 是连续型；

9. JS 散度
   也是度量两个概率分布的相似度，具有对称性，取值在 0 到 1 之间；
   \(\begin{align} D_{\mathrm {JS}}(P\|Q) = \frac{1}{2} KL(P\| \frac{P+Q}{2} + \frac{1}{2} KL(Q\| \frac{P+Q}{2}) \end{align}\)
   两个分布 $P$, $Q$ 离得很远，完全没有重叠的时候，那么 KL 散度值是没有意义的，而 JS 散度值是一个常数；

10. Wasserstein 距离
    度量两个概率分布的距离；
    \(\begin{align} W_{n}(P ,Q) &= \left(\inf_{\gamma \in \Gamma(P, Q)} \int_{M \times M} d(x,y)^n d\gamma (x,y) \right)^{1/n} \\ W(P ,Q) &= \inf_{\gamma \in \Gamma(P, Q)} \mathtt E_{x, y} \sim \gamma[\lVert{x-y}\rVert] \end{align}\)
    $\Gamma(P, Q)$ 是分布 $P$ 和 $Q$ 所有可能的联合分布；从该分布中采样到样本对 $(x, y)$，取到样本距离的最小均值，就是 Wasserstein 距离；直观上来看就是分布 $P$ 变换到分布 $Q$ 时在最优路径规划下的最小消耗；所以 Wesserstein 距离又叫 Earth-Mover 距离或推土机距离；
    Wessertein 距离的优势在于：即使两个分布没有重叠或者重叠非常少，仍然能反映两个分布的远近；

2.1.4 博弈论

1. 纳什均衡
   一个经济学和博弈论的术语，代表一着个系统的稳定状态，此时系统的任何一个参与者都无法通过各自行动的改变而增加收益；

图1：木桶效应 

2.2 卷积网络

• 全连接
  多层感知机
• 卷积
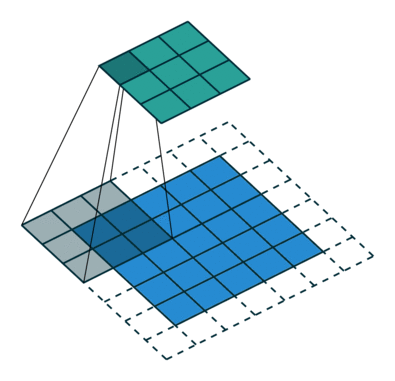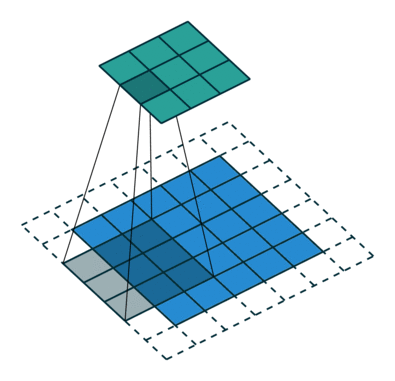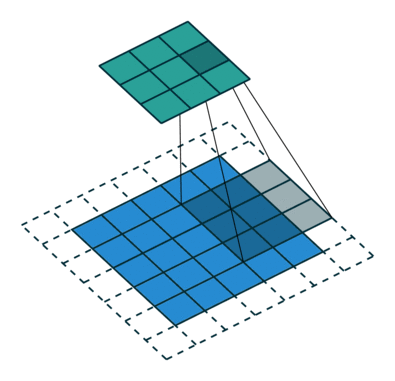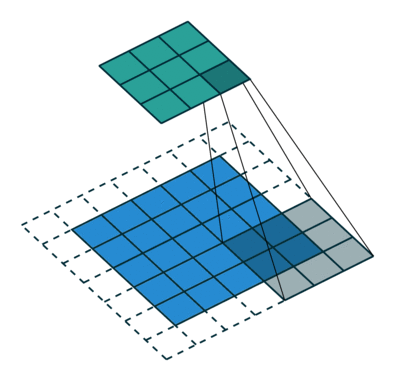
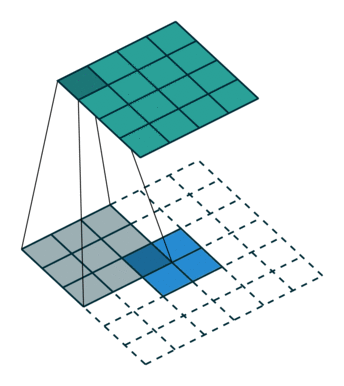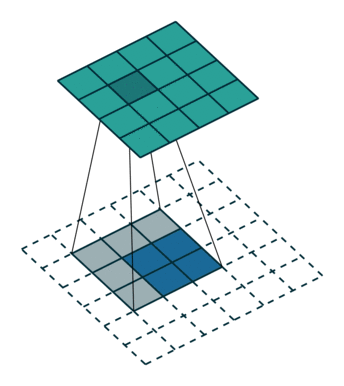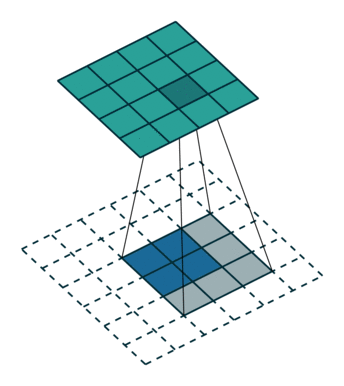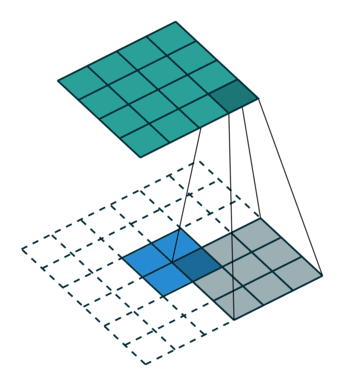
  下采样，权重共享，步长，跨步卷积，特征图

卷积	反卷积	微步卷积

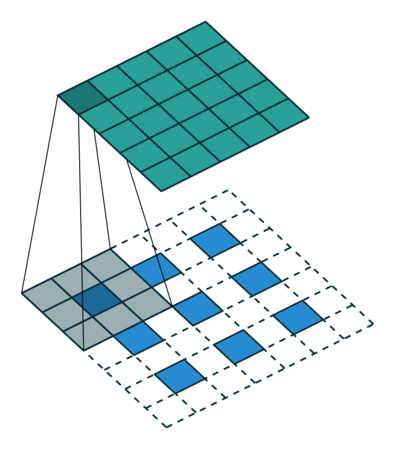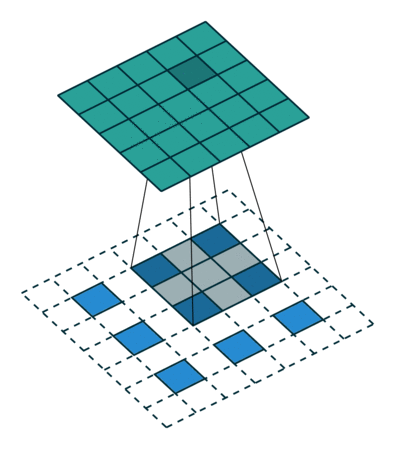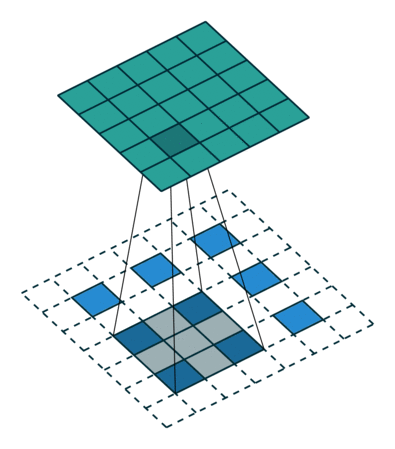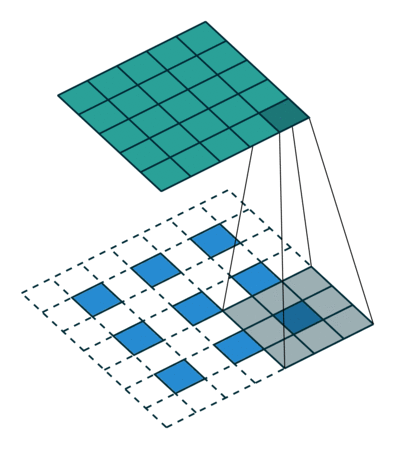• 反卷积 转置卷积、微步卷积；目的是上采样；
  在超分辨率，分割，深度估计，光流计算，自编码，GAN等场景中有这广泛应用；（事实上需要输出图像的地方都需要他）
• 池化
• 激活函数
  Sigmoid 函数：
  $S(t)=\frac{1}P{1+e^{−t}}$
  • 定义域：$(-\infty, +\infty)$
  • 值域：(−1, 1)
  • 函数在定义域内为连续和光滑函数
  • 处处可导，导数为：$f'(x) = f(x)(1−f(x))$
• 损失函数
  交叉熵损失²：$Loss = - \sum_{i=1}^N [y_i \log P(x_i) + (1-y_i) \log (1 - P(x_i))]$
  对于二分类问题，令样本标签为 $y$，预测为正样本（真）的概率记为 $P(x) = P(y=1|x)$，显然预测为负样本的概率为 $P(y=0|x) = 1 - P(y=1|x)$，两公式整合在一起就是：
  \(\begin{align} P(y\|x) &= P(y=1\|x)^y \cdot (1 - P(y=1\|x))^{1-y} \\ \log P(y\|x) &= y \log P(y=1\|x) + (1-y) \log (1 - P(y=1\|x)) \\ &= y \log P(x) + (1-y) \log (1 - P(x)) \label{log_label}\\ \end{align}\) 最终希望公式 $\eqref{log_label}$ 的值越大越好；于是将 loss 函数定义为：
  \(\begin{align} L_{single} &= - [y \log P(x) + (1-y) \log (1 - P(x))] \label{loss_single}\\ L_{multi} &= - \sum_{i=1}^N [y_i \log P(x_i) + (1-y_i) \log (1 - P(x_i))] \label{loss_multi}\\ \end{align}\) 公式 $\eqref{loss_single}$ 是单个类别的情况，公式 $\eqref{loss_multi}$ 是多个类别的；
  1. :o: 为什么要加 log
     除了方便化简外，也是因为 $\log$ 的值域是 $(-\infty, +\infty)$；
• RNN & LSTM

---

End

附录

A 参考资料

1. Ian Goodfellow, et. al. 著 赵申剑 等译. 深度学习[M]. 北京:人民邮电出版社, 2017. ↩

2. rtygbwwwerr. 交叉熵[EB/OL]. https://blog.csdn.net/rtygbwwwerr/article/details/50778098. 2016-03-03/2019-04-15. ↩