4 minute read

译自：Meta-Learning: Learning to Learn Fast https://lilianweng.github.io/lil-log/2018/11/30/meta-learning.html，有增删
元学习，又叫“学会学习”，旨在通过少量样本的 fine-tuning 快速设计出具有类似属性的机器学习模型；甚至，推广到在训练期间从未遇到过的新任务和新环境；这就是元学习也被称为学习如何学习的原因；「元」指的是内在的知识，以便扩展到新的同类任务；

旨在通过少量样本的fine-tuning，使该模型可以适应训练样本中没有遇到的新任务和新环境 跟 finetuning 有啥区别啊

全文逻辑需要重整，感觉都没有逻辑了

说明：尽管大量科研相关人员已经标注了很多标准数据集。但就算著名如ImageNet，在其千万级数据集中也不过分为21841 个类别，现实世界中已经标注的数据仍然只占少数，且有诸多场景如疾病图像的数据难以大量获取。
故研究在目标域无标注数据的情况下，如何进行有效的学习并进行预测将非常有意义。

常见的方法：

  • 1）「基于度量」学习有效的距离度量;
  • 2）「基于模型」使用（循环）网络与外部或内部存储器;
  • 3）「基于优化」明确优化模型参数以进行快速学习；

常见的方向：

  • 1）无监督学习
    • 小样本学习
    • 单样本学习
    • 零样本学习
  • 2）监督学习
  • 3）强化学习

几个元学习的具体示例：

  • 在不包含猫的训练集上训练出的模型，在输入少量猫的图像后就可以识别猫；
  • 游戏机器人能够快速掌握新游戏；
  • 一个只在平地环境训练过的机器人，可以完成上坡的任务；

1 元学习

本文以监督学习为例探讨元学习，元强化学习不做赘述；

1.1 一个简单的视角

小样本分类，又叫 Few-shot classification 或 k-shot classification，是监督学习领域中元学习的代表； 与常规分类任务不同的地方在于，小样本分类可以预测出训练集中未出现过的类别，不过需提供额外的 support set 来辅助分类； few-shot classification 和 k-shot classification 是一回事吗？这里的可识别未知样本，指的是对网络未知，但对模型调用者是已知的
该想法在某种程度上类似于模型预训练或 fine tuning；但 fine tuning 是针对新任务进行具体的模型优化，模型能力更具体化了；而元学习则是旨在训练出一个具有较强泛化能力的模型，以完成对未知类别的分类；感觉这段对比写的不够明显
如下图所示：
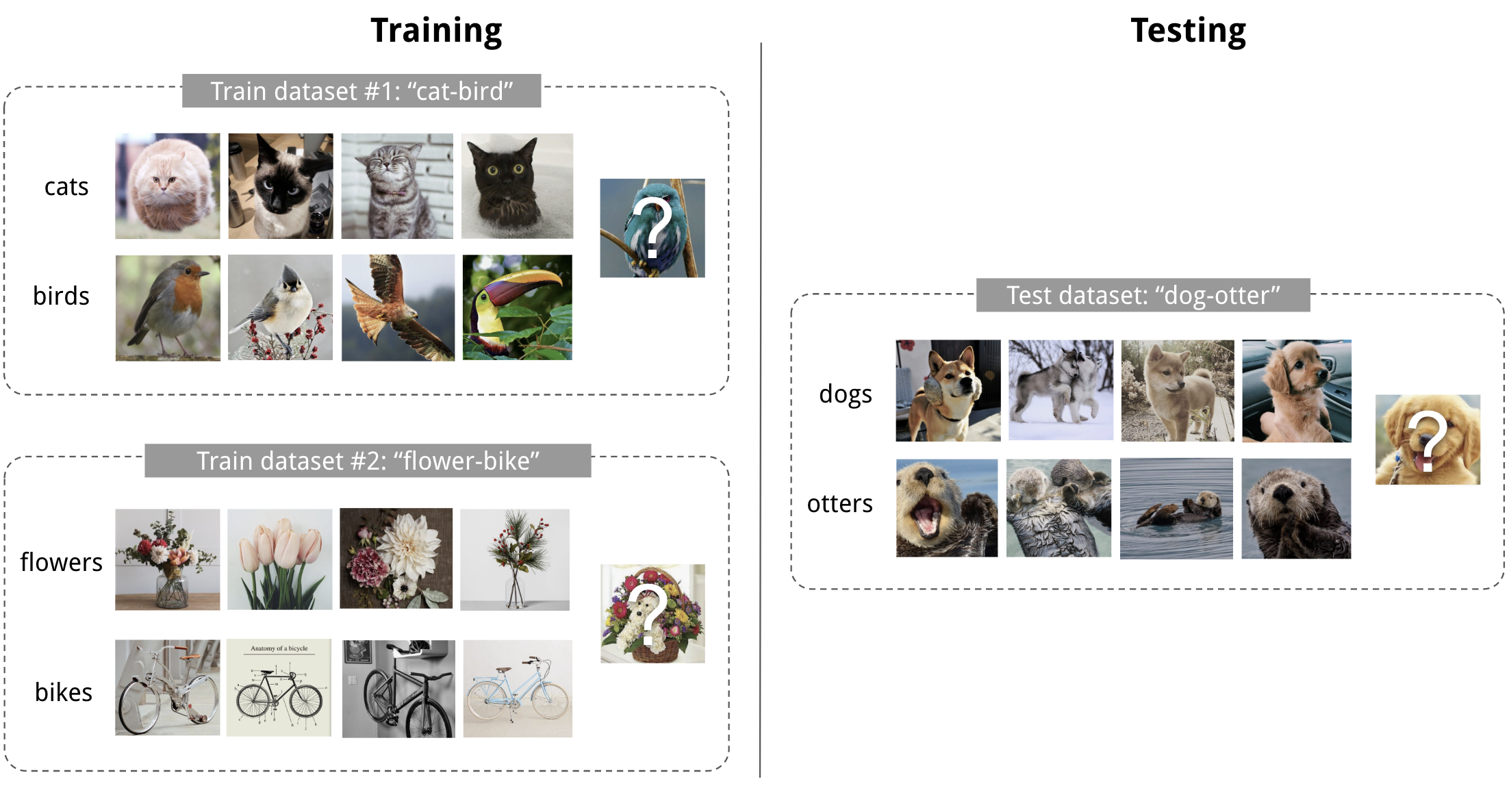图 1. 4-shot 2-class image classification 的示例 (图片来源 Pinterest)

常见的方法：

  基于模型 基于度量 基于优化
核心思想 RNN，memory 度量学习 梯度下降
\(P_\theta(y|\mathbf{x})\) 是如何被建模的 \(f_\theta(\mathbf{x}, S)\) \(\sum_{(\mathbf{x}_i, y_i)\in S}{k_\theta(\mathbf{x}, \mathbf{x}_i)y_i}\) (*) \(P_{g_\phi(\theta, S^L)}(y|\mathbf{x})\)

(*)：\(k_\theta\) 是衡量 \(\mathbf{x}_i\) 和 \(\mathbf{x}\) 相似性的函数；
看不懂，但是感觉很重要

2 基于度量的元学习

根据输入来得到一个嵌入向量，然后基于嵌入向量来设计合适的度量函数；

Metric-Based 的核心思想类似于最近邻算法（即，k-NN和k 均值聚类）和核密度估计； 样本的预测概率是其与 support set 上样本相似度的加权和； ；
\(P_\theta(y \vert \mathbf{x}, S) = \sum_{(\mathbf{x}_i, y_i) \in S} k_\theta(\mathbf{x}, \mathbf{x}_i)y_i\)，\(k_\theta\) 为计算两个样本相似度的函数；
基于度量的元学习的核心就是学习一个好的特征表达模型；基于度量的学习与此意图完全一致，因为它旨在学习对象的度量或距离函数；

metric function, kernel function, distance function 说的都是一个东西；

2.1 挛生网络

用图像验证的方法来处理样本图像分类（one-shot classification）问题；
这个方式其实是将未知类别的待测试样本与给定的 support set 进行关联，相似度最高的即为该类别；并非真正意义上判断出这个类别是新的类别，如果加上一个阈值来判断是否出现新类别也可以，只是这个阈值的确定似乎是复杂的；

挛生网络1是用来学习输入数据样本对之间关系的网络，输入的样本数据对依次经过网络，得到两组特征，通过计算他们的联合损失来训练网络；

Koch，Zemel和Salakhutdinov（2015）2提出了使用挛生网络进行「单样本图像分类」的方法；整体思路是，按图像验证任务进行训练，测试时将测试图和训练集中所有图片一一比对，取与之相似读最高的训练样本的类别为测试图类别； 不就是化分类为验证吗，而且是以牺牲速度为代价，为啥要起个元学习这么高大上的名字

挛生网络简述：

  • 输入两张图像，通过 CNN 网络后在 embedding 层（\(f_\theta\)）提取一对特征向量 \(f_\theta(\mathbf{x}_i)\) 和 \(f_\theta(\mathbf{x}_j)\)；
  • 计算两个特征向量的 \(L1\) 距离 \(D = \vert f_\theta(\mathbf{x}_i) - f_\theta(\mathbf{x}_j) \vert\)
  • 接一个全连接层 和 Sigmoid，将距离转换为概率 p；
  • 因为是二分类，所以我们用交叉熵作为损失函数；
    \(% <![CDATA[ \begin{aligned} p(\mathbf{x}_i, \mathbf{x}_j) &= \sigma(\mathbf{W} * \mathbf{D}) \\ \mathcal{L}(B) &= \sum_{(\mathbf{x}_i, \mathbf{x}_j, y_i, y_j)\in B} \mathbf{1}_{y_i=y_j}\log p(\mathbf{x}_i, \mathbf{x}_j) + (1-\mathbf{1}_{y_i=y_j})\log (1-p(\mathbf{x}_i, \mathbf{x}_j)) \end{aligned} %]]>\)
    注：\(B\) 是训练时的单个批次； \(L1\) 距离可以换做其他距离，比如欧式距离（\(L2\)）、夹角余弦等；
    预测结果 \(\hat{c}_S(\mathbf{x}) = c(\arg\max_{\mathbf{x}_i \in S} P(\mathbf{x}, \mathbf{x}_i))\)， 其中 \(S\) 为 support set，\(\mathbf{x}\) 为测试图像，\(c(\mathbf{x})\) 为 \(\mathbf{x}\) 的标签    ；


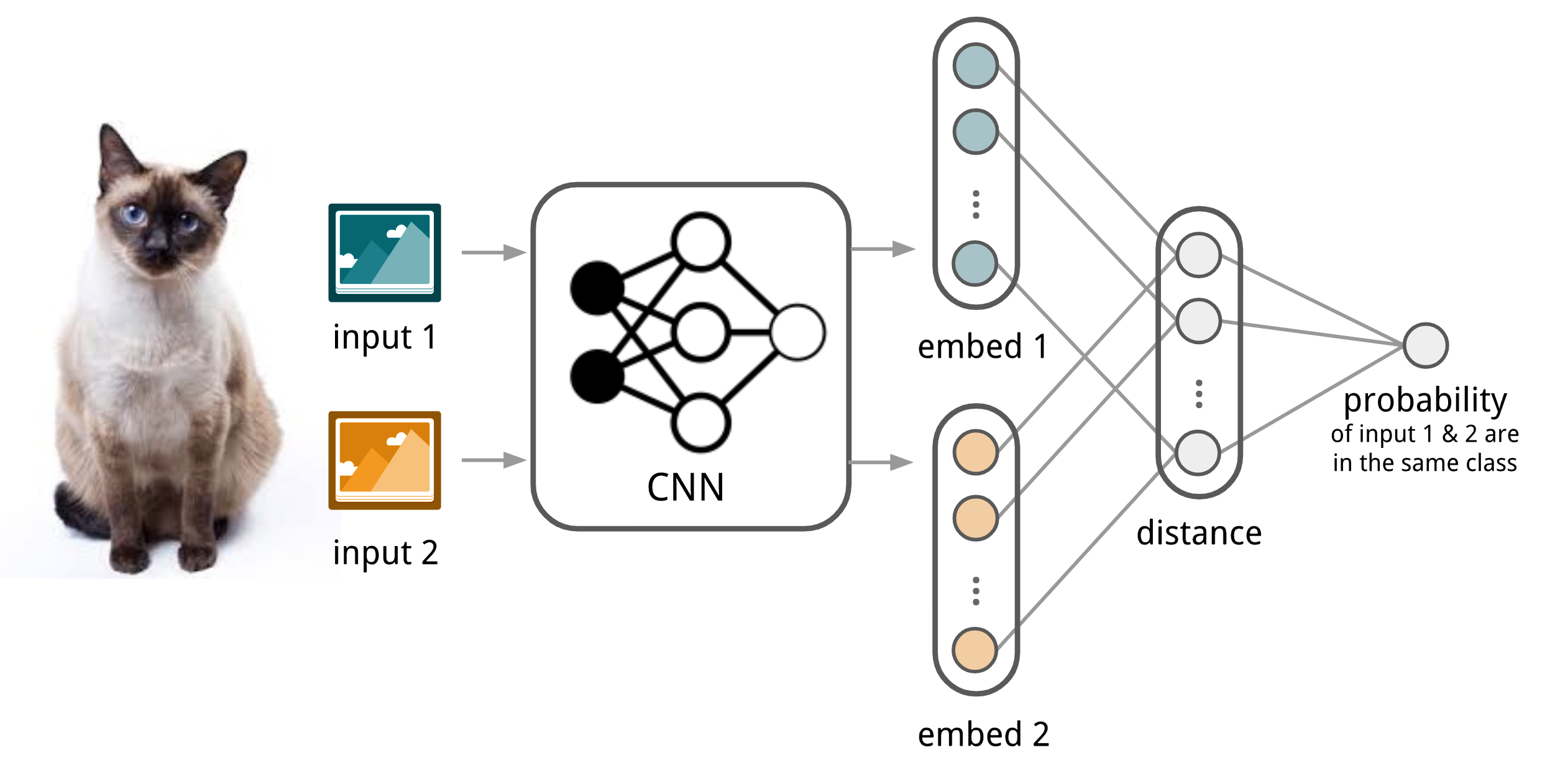
图 2. 小样本分类中挛生网络的结构

假设学习到的特征提取函数 \(f_\theta\) 可以对未知类别进行分类，这和迁移学习中的预训练（fine tuning）相似，只不过如果新任务和原任务特征偏差较大时，预训练效果会变差；此处没有阐述元学习为啥会好啊

2.2 匹配网络

Matching Networks(Vinyals et al., 20163)，是为了学习出一个针对任意给定的 support set 都可以进行分类的网络；
看不出来，跟挛生有啥区别；核心都在于 embedding ，非整出来个 挛生和匹配

相似度：\(a(\mathbf{x}, \mathbf{x}_i) = \frac{\exp(\text{cosine}(f(\mathbf{x}), g(\mathbf{x}_i))}{\sum_{j=1}^k\exp(\text{cosine}(f(\mathbf{x}), g(\mathbf{x}_j))}\)
归一化的时候为什么不直接求和，而要用 softmax呢，夹角余弦值域很明显啊，为啥要多做一个处理 分类网络：\(c_S(\mathbf{x}) = P(y \vert \mathbf{x}, S) = \sum_{i=1}^k a(\mathbf{x}, \mathbf{x}_i) y_i {,} S=\{(\mathbf{x}_i, y_i)\}_{i=1}^k \text{ is support set}\)，\(f\) 为作用于测试样本的 embedding function，\(g\) 为作用于support set 的 embedding function
为什么要乘以 $$y_i$$不是 k-shot n-class 吗，为什么感觉 k 像是整个 support set 的数据量


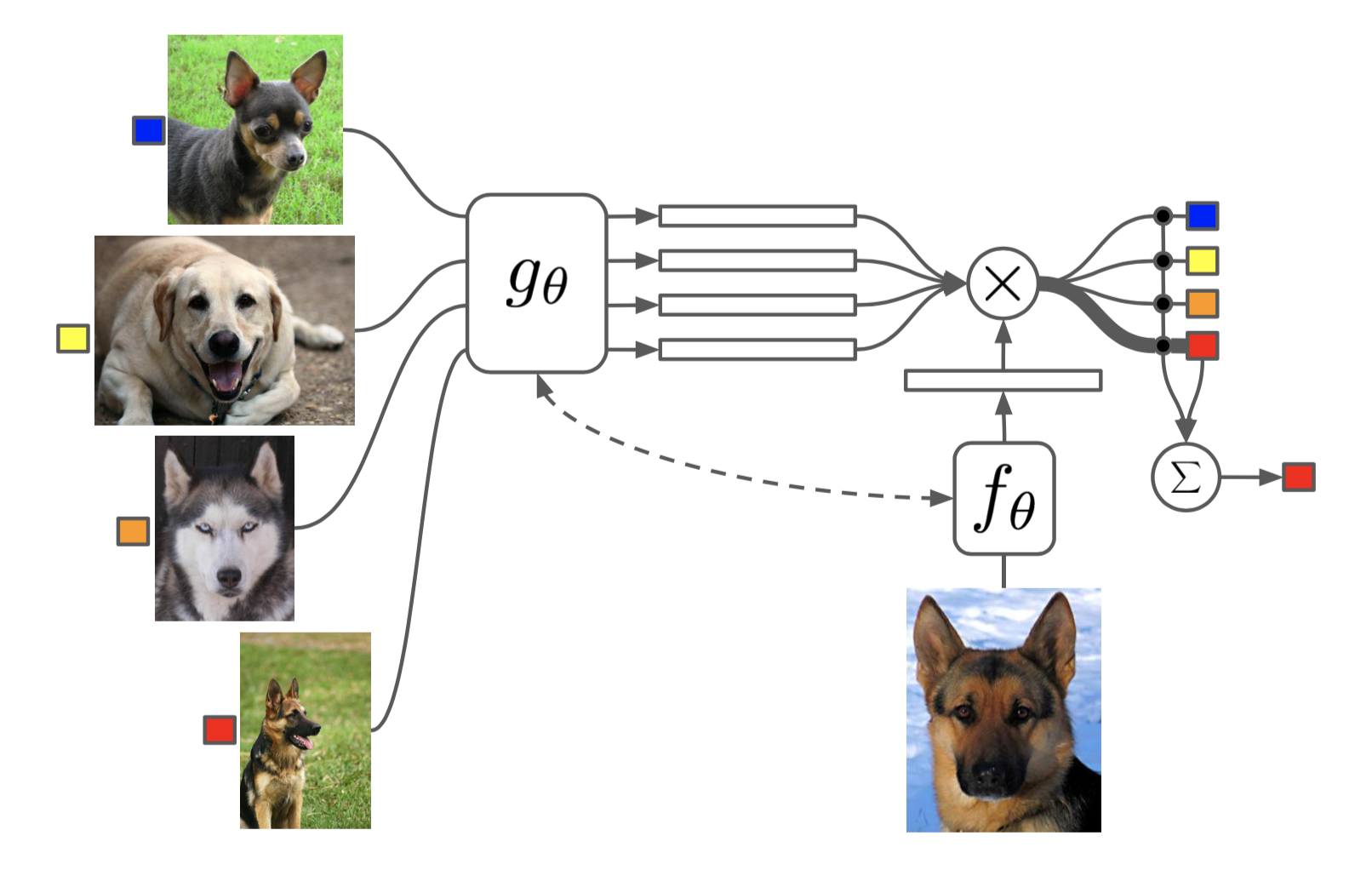
图 3. Match Net 结构图3

（1）简单嵌入
简单的 Matching Networks 中，embedding 向量 来源于神经网络和单个输入样本；此时 \(f = g\)；

（2）全上下文嵌入（FCE）
将整个 support set 作为注意力模型的输入，使得可以基于与其他 support 样本的关系来调整 embedding 的效果，以提高 embedding function 的性能；

  • \(g_\theta(\mathbf{x}_i, S)\) 使用双向 LSTM 在整个 support set \(S\) 上对 \(\mathbf{x}_i\in S\) 进行编码；
  • \(f_\theta(\mathbf{x},S)\) 使用 LSTM 对测试样本编码，并结合 \(S\) 上的注意力来计算相似度；
    细节读的不是很懂4

该方法对于较难的任务（比如在 mini ImageNet 上进行小样本分类）确实有精度提升，但在简单任务上没有任何区别；
Matching Networks 的训练过程旨在与测试时的推理匹配翻译的有问题；他修正了训练和测试条件应该匹配的观点；

2.3 关系网络

Relation Network (RN)(Sung et al., 20184) 和挛生网络有些相似，但也有如下不同：

  • 相似度不是基于 \(L1\) 距离，而是由 CNN 网络（\(g_\phi\)）计算得到；
  • 使用 MSE 损失代替 Softmax，因为相似度度量更像是回归，而不是二分类；\(\mathcal{L}(B) = \sum_{(\mathbf{x}_i, \mathbf{x}_j, y_i, y_j)\in B} (r_{ij} - \mathbf{1}_{y_i=y_j})^2\)


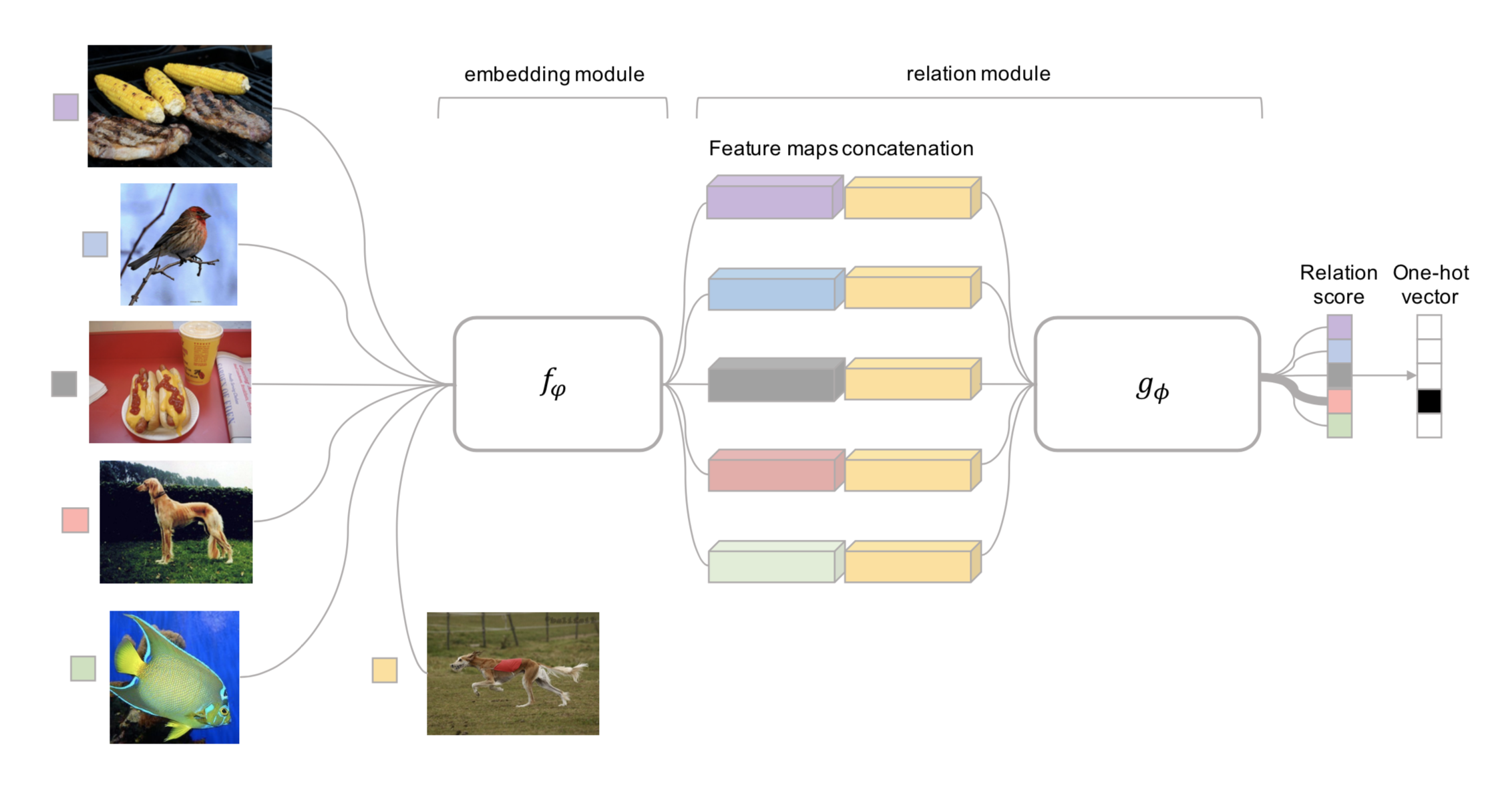
图 4.一个 5-way 1-shot（5分类单样本） 的关系网络结构图4

有一篇 DeepMing 出的关于关系推理的关系网络，别弄混了；

2.4 原型网络

Prototypical Networks (Snell, Swersky & Zemel, 20175)针对 support set 中的每个类，取该类嵌入特征的均值作为该类别的嵌入特征；此嵌入特征被成为该类的原型特征向量： \(\mathbf{v}_c = \frac{1}{|S_c|} \sum_{(\mathbf{x}_i, y_i) \in S_c} f_\theta(\mathbf{x}_i)\)，\(\mathcal{C}\) 为 support set 中的类别，\(c \in \mathcal{C}\)，\(f_\theta\) 为 embedding function； 测试样本 \(x\) 在 support set 上的分布为：
\(P(y=c\vert\mathbf{x})=\text{softmax}(-d_\varphi(f_\theta(\mathbf{x}), \mathbf{v}_c)) = \frac{\exp(-d_\varphi(f_\theta(\mathbf{x}), \mathbf{v}_c))}{\sum_{c' \in \mathcal{C}}\exp(-d_\varphi(f_\theta(\mathbf{x}), \mathbf{v}_{c'}))}\)


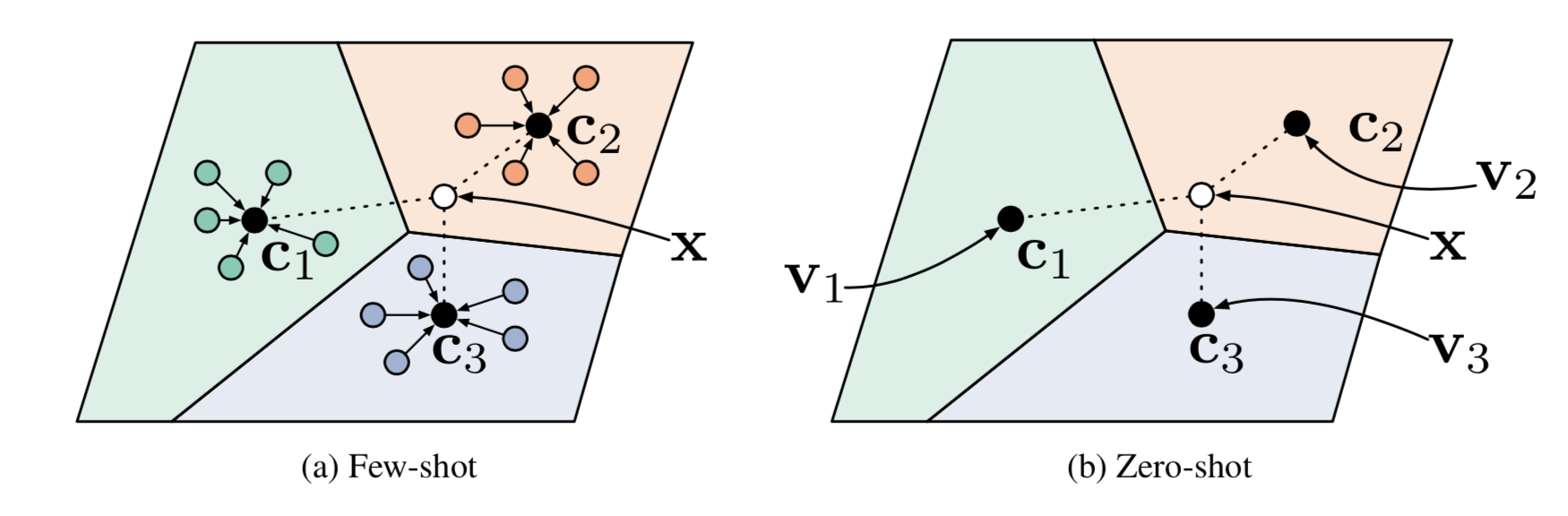
图 5.零样本和小样本原型网络结构图5

其中 \(dφ\) 可以是任何距离函数，只要 \(φ\) 是可微分的；论文中使用了欧氏距离的平方；
损失函数为：\(\mathcal{L}(\theta) = -\log P_\theta(y=c\vert\mathbf{x})\)

3 基于模型的元学习

Model-Based 方法是设计一个经过几轮迭代就可以更新好参数的快速学习的模型；这种快速更新机制可以通过模型内部的结构或其他元学习模型来控制；

3.1 记忆增强神经网络

这一段感觉好多翻译都不地道啊 Memory-Augmented Neural Networks（MANN）是使用一组利用外部存储器来强化神经网络训练过程的网络结构，常见的有神经图灵机（Neural Turing Machines，NTM） 和记忆网络（Memory Networks）6；他们使用显式的外部存储帮助网络快速地合并新信息；而像 vanilla RNN 和 LSTM 这样只有内部记忆的 RNN 网络并不能作为 MANN；
基于神经图灵机，Santoro et al. (2016)7 针对训练和内存检索（或者叫寻址机制，取决与怎么把注意力参数写入内存）提出了一些新方法；
（1）MANN 的训练过程
\((\mathbf{x}_{t+1}, y_t)\) 没弄明白，他的精髓在哪里 （2）元学习的寻址机制
基于内容的寻址机制让模型处理元学习时更稳定；

  • 从内存读
    \(\mathbf{k}_t\) 为 \(t\) 时刻样本的特征向量，那么读取到的向量：\(\mathbf{r}_i = \sum_{i=1}^N w_t^r(i)\mathbf{M}_t(i) \text{, where } w_t^r(i) = \text{softmax}(\frac{\mathbf{k}_t \cdot \mathbf{M}_t(i)}{\|\mathbf{k}_t\|_2^2 \cdot \|\mathbf{M}_t(i)\|_2^2 })\)
    \(M_t(i)\) 是内存中矩阵的第 $i$ 条向量；

  • 往内存写

3.2 元网络

Meta Networks(MetaNet) Munkhdalai & Yu, 20178
（1）Fast Weights
（2）模型结构
（3）训练策略

4 基于优化的元学习

4.1 LSTM

Ravi & Larochelle (2017) 9将原始的模型成为「学习者」（learner），将用来指导「学习者」网络在小数据集上快速更新参数的网络称为「元学习者」（meta-learner）；
（1）为什么要选用 LSTM
（2）模型结构

4.2 跨模型元学习

Model-Agnostic Meta-Learning（MAML）10
（1）一阶 MAML
First-Order MAML (FOMAML)

4.3 Reptile11

（1）最优化假设
（2）Reptile vs FOMAML

5 应用

  1. 分类
    在没有任何训练样本的情况下，借助辅助知识（如属性、词向量、文本描述等）学习一些从未见过的新概念；
  2. 翻译
    已知 A 到 B，B 到 C 的翻译，可自动学习出 A 到 C 的翻译；
  3. 图像合成
    能够合成从未见过的类别图像；
  4. 图像哈希
    在已知类别上学到哈希算法能够运用到新的未知类别上；

6 思考

1.用神经网络学习来生成网络结构

TOP

附录

A 名词解释

1. K-shot N-class classification
每个类别有 K 个训练样本的 N 分类问题；

2. support set
一个包含多个类别标签的数据集 \(S\)，他的单个类别样本数一般都比较少；\(S\) 数据集中的标签在训练过程中是完全没有出现过的；网络会基于 \(S\) 为测试集进行分类，预测的标签就来源于这个数据集；

3. embedding 这段解释好像是有问题的 该操作意在不需要网络输出直接的结果，而是时候最后一个可用的 feature map；由之派生而来的 embedding layer，embedding vector，embedding function； 以分类网络为例，embedding 层指的是产生分类的上一层；该层输出的特征叫做 embedding vector，可简单译作「嵌入特征」；去掉了分类层的网络就是 embedding function；

4. few-shot classification
小样本分类，包括 k-shot classification 和 one-shot classification；

5. 强偏置问题
训练过程中为出现过的样本，会被强制归类为出现过的样本；

B 资料

  1. Oriol Vinyals 在 NIPS 2018 中的演讲
  2. Brenden M. Lake, Ruslan Salakhutdinov, and Joshua B. Tenenbaum. “Human-level concept learning through probabilistic program induction.” Science 350.6266 (2015): 1332-1338.
  3. Oriol Vinyals’ talk on “Model vs Optimization Meta Learning”
  4. Gregory Koch, Richard Zemel, and Ruslan Salakhutdinov. “Siamese neural networks for one-shot image recognition.” ICML Deep Learning Workshop. 2015.
  5. Alex Graves, Greg Wayne, and Ivo Danihelka. “Neural turing machines.” arXiv preprint arXiv:1410.5401 (2014).
  6. Chelsea Finn’s BAIR blog on “Learning to Learn”.
  7. Slides on Reptile by Yoonho Lee.
  8. DeepLearning Zero Shot Learning 零样本学习
  9. What is zero-shot learning?
  10. Applications of Zero-Shot Learning
  11. 零样本学习入门指南
  12. one/zero-shot learning（零样本学习）的理解
  13. Zero-shot learning（零样本学习）
  14. 零样本学习·「了解」

C 参考文献

  1. Bromley, Jane, Bentz, James W, Bottou, Leon, Guyon, Isabelle, LeCun, Yann, Moore, Cliff, Sackinger, Eduard, and Shah, Roopak. Signature verification using a siamese time delay neural network. International Journal of Pattern Recognition and Artificial Intelligence, 7(04):669–688, 1993. ↩

  2. G Koch, R Zemel, and R Salakhutdinov. Siamese neural networks for one-shot image recognition. In ICML Deep Learning workshop, 2015. ↩

  3. Vinyals, Oriol et al. Matching Networks for One Shot Learning. NIPS (2016) arXiv preprint arXiv:1606.04080. ↩ ↩2

  4. Flood Sung, et al. Learning to Compare: Relation Network for Few-Shot Learning. In CVPR, 2018. arXiv:1711.06025. ↩ ↩2

  5. Jake Snell, Kevin Swersky, and Richard Zemel. Prototypical Networks for Few-shot Learning. CVPR. 2018. arXiv:1703.05175. ↩ ↩2

  6. J Weston, et al. Memory Networks. 2014. arXiv:1410.3916. ↩

  7. A Santoro, S Bartunov, M Botvinick, D Wierstra, and T Lillicrap. Meta-Learning with Memory-Augmented Neural Networks. In ICML, 2016. ↩

  8. Munkhdalai, Tsendsuren and Yu, Hong. Meta networks. International Conferecence on Machine Learning(ICML), 2017. arXiv:1703.00837. ↩

  9. Ravi, S. and Larochelle, H. (2017). Optimization as a model for few-shot learning. In the International Conference on Learning Representations (ICLR). ↩

  10. Chelsea Finn, Pieter Abbeel, and Sergey Levine. Model-agnostic meta-learning for fast adaptation of deep networks. ICML 2017. arXiv preprint arXiv:1703.03400. ↩

  11. Alex Nichol, Joshua Achiam, John Schulman. On First-Order Meta-Learning Algorithms. arXiv preprint arXiv:1803.02999 (2018). ↩

Comments

You May Also Enjoy