「DL」 梯度下降
1 概念
梯度方向导数最大;
经验风险最小化:最小化平均误差;
批量梯度下降:一次迭代使用所有训练数据;
小批量梯度下降:一次迭代使用部分训练数据;
随机批量梯度下降:一次迭代使用一个训练数据;现在常用来表示小批量梯度下降;
2 挑战
| 挑战 | 描述 | 监测 | 方案 |
|---|---|---|---|
| 病态 | 数值优化中普遍的问题,即使很小的更新步长也会增加代价函数; | 梯度的2范数在持续增加,:ghost: | 减小学习率缓解 牛顿法(不适合CNN) |
| 局部极小值 | 梯度的范数(可能) | 更多的数据; 更小的网络; 没那么重要 |
|
| 平坦区域(高原、鞍点) | CNN 出现鞍点的概率是局部极小点的指数倍; | 一阶对鞍点适应性较好; | |
| 悬崖、梯度爆炸 | 循环网络中最常见 | 梯度截断 | |
| 长期依赖 | 同一数据被反复累乘 | 易造成梯度消失和爆炸 |
自编码网络只有全局极小和鞍点,没有局部极小;因为输入到输出是线性映射;为啥线性就不会有局部极小值;也不是严格的线性吧
时间步长上的累乘,造成循环网络易出现悬崖式梯度
3 一阶
梯度下降
3.1 基础算法
GD:每次使用一个样本,容易陷入局部最优,且训练速度慢;
SGD:其实是批量随机梯度下降,能轻易逃脱鞍点为什么;
动量:以累计梯度按比例对梯度进行衰减;主要解决病态问题和随机梯度的方差;可以很好的穿过狭长的峡谷;而 SGD 容易在窄轴上来回震荡;
Nesterov动量:使用更新后的权重计算梯度;在批量梯度中收敛速度减少,但 SGD 中没有变化;
3.2 自适应学习率
| 方法 | 功能 | 特色 | 策略 |
|---|---|---|---|
| AdaGrad | 学习率衰减 | 学习率自适应反比于累计梯度(计算时用了平方和的平方根) | |
| RMSProp | 学习率动态衰减 | 更好应对非凸 | 使用指数6衰减平均代替简单的累计,以防止到达凸结构之前就将学习率衰减太小,导致学习缓慢; |
| AdaDelta | 无需设置全局学习率 | - | |
| Adam | 对超参更鲁棒 | 将修正操作同时作用于一阶矩和二阶矩; |
关于优化算法的选择尚没有确定的结论;
4 二阶近似
牛顿法;缺点是无法适应鞍点问题,也有一些方案,如无鞍点牛顿法;但二阶在 CNN 中应用仍少;当然,对于极大值也无法适应;
共轭梯度;
BFGS;
5 对比
那种优化器最好,该选择哪种优化算法,目前还没能够达达成共识;Schaul et al (2014)展示了许多优化算法在大量学习任务上极具价值的比较;虽然结果表明,具有自适应学习率的优化器表现的很鲁棒,不分伯仲,但是没有哪种算法能够脱颖而出;
目前,最流行并且使用很高的优化器(算法)包括SGD、具有动量的SGD、RMSprop、具有动量的RMSProp、AdaDelta和Adam。在实际应用中,选择哪种优化器应结合具体问题;同时,也优化器的选择也取决于使用者对优化器的熟悉程度(比如参数的调节等等);
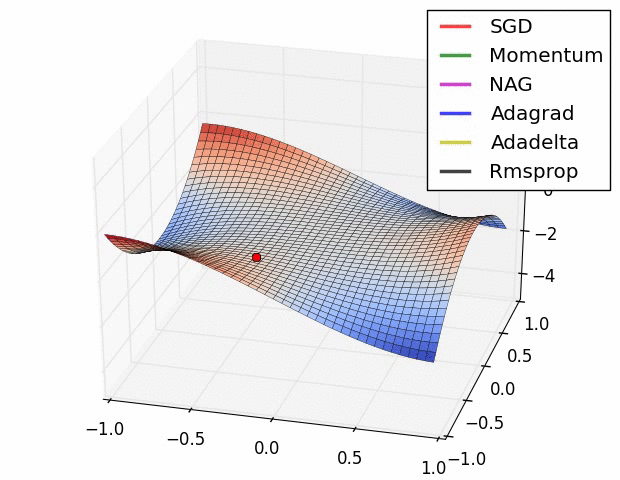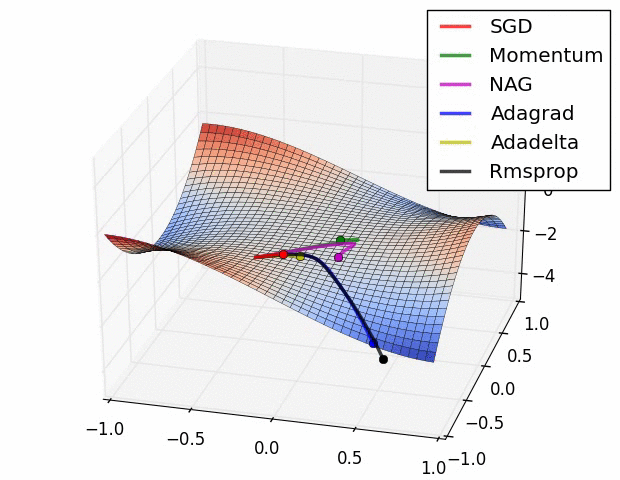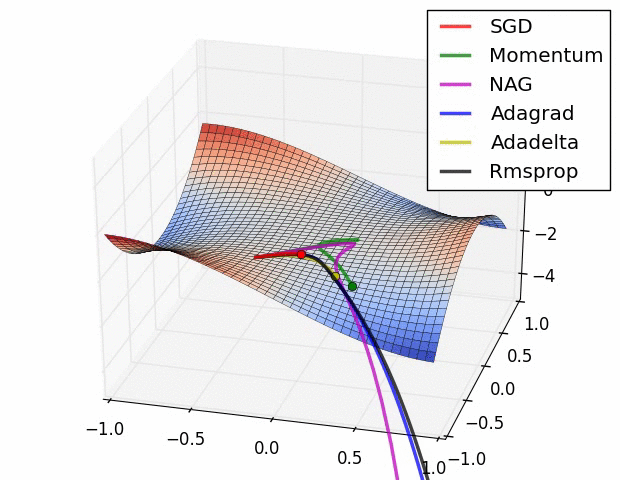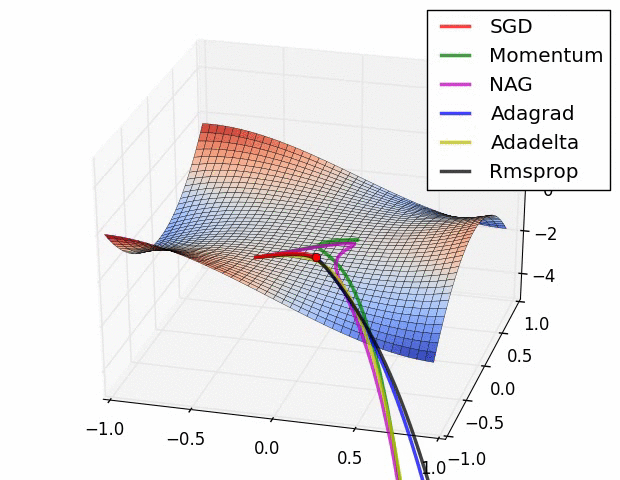
图1:常规梯度下降
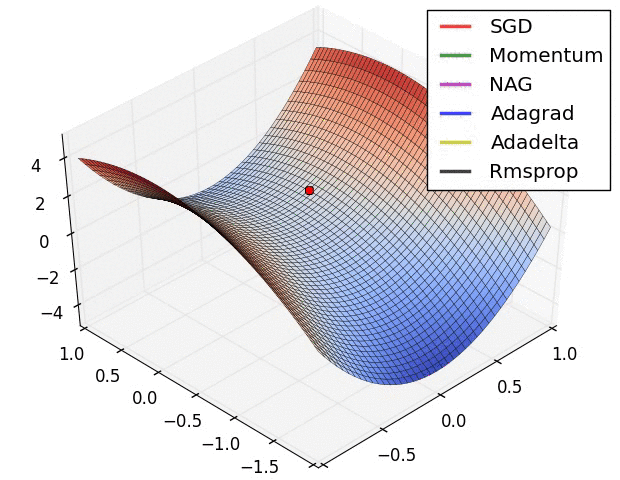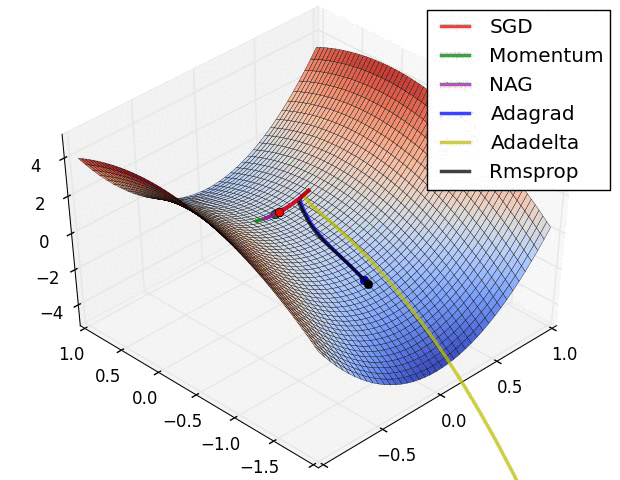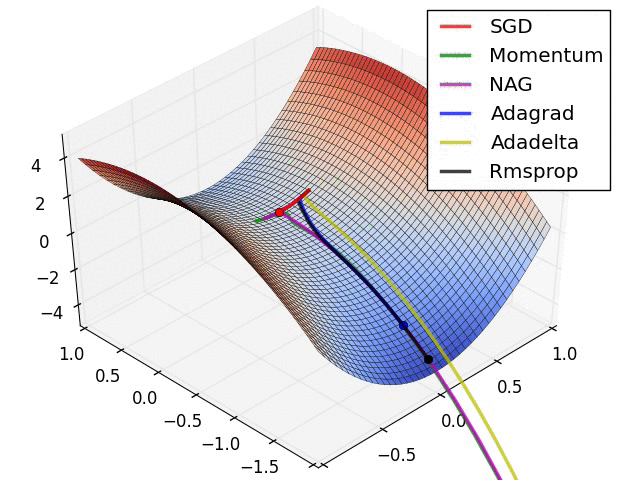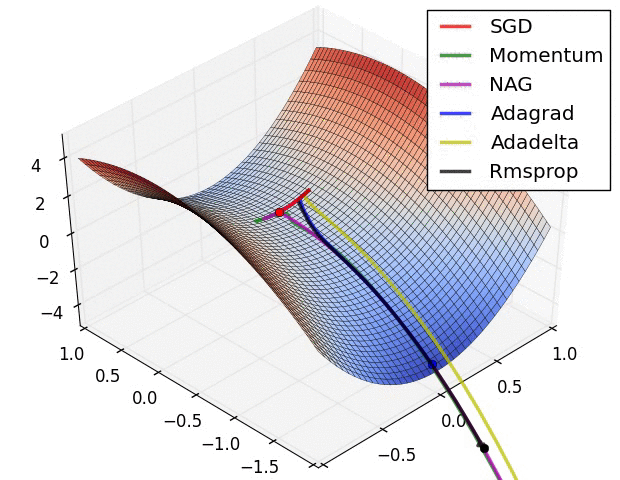
图2:鞍点问题
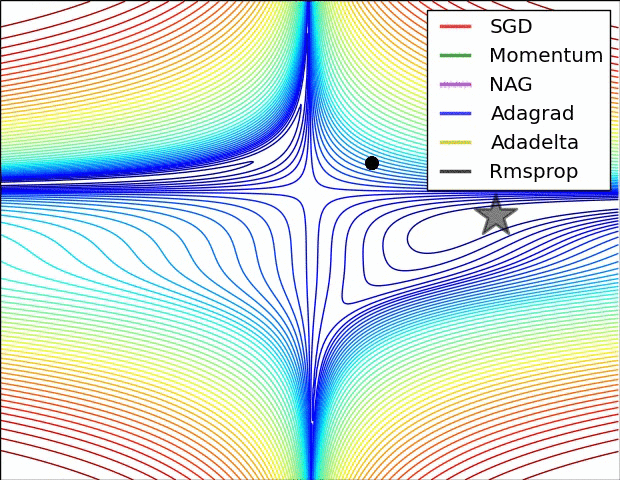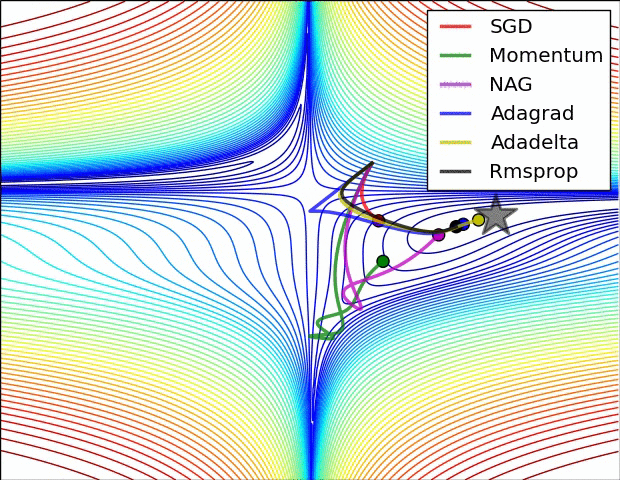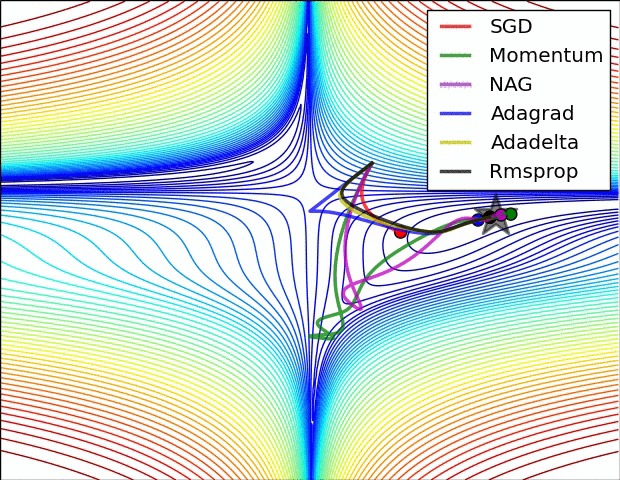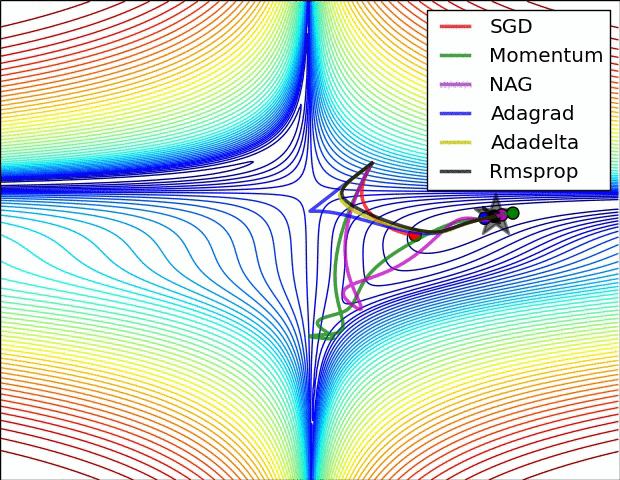
图3:复杂情况
Comments