1 minute read

「卷积」通常是「参数共享卷积」的简称；且该卷积与数学中的卷积操作不是一个概念；
除了图像和视频等处于欧几里得空间的数据之外，更多的数据是处于非欧几里得空间的，例如社交网络中的关系数据、三维点云数据、分子结构数据、基因数据和交通数据等等；由于这些数据的无序性和维度的可变性，使得传统卷积很难应用其中；
当然，所有的卷积都是在探讨如何对局部数据按照某一个操作聚合，不同的操作方式就对应于不同的卷积；

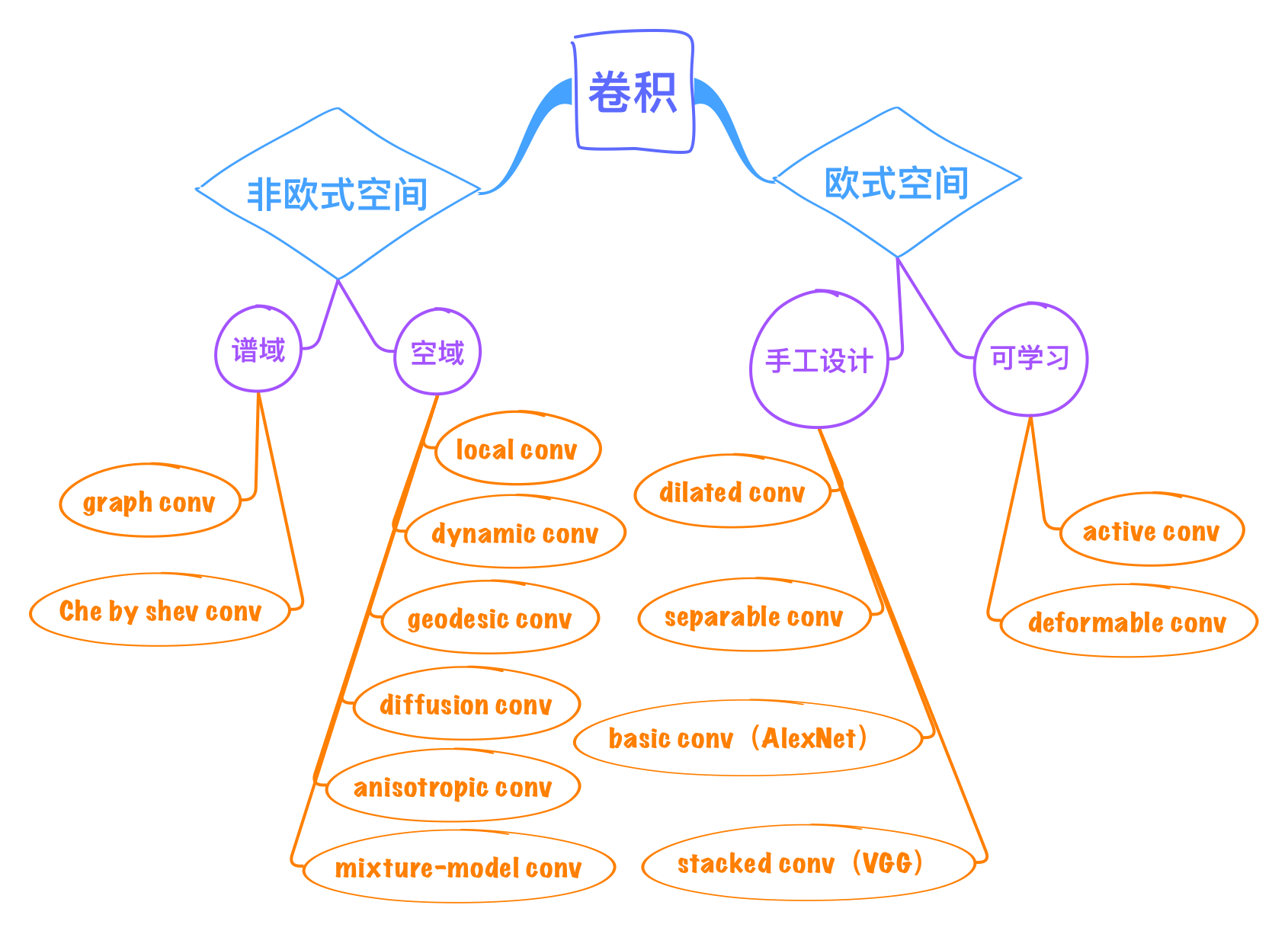图1. 常见卷积模型

1 卷积

卷积，其本质是局部数据的一个聚合操作；学习卷积核就是在学习局部聚合参数的过程；
卷积由局部结构确定的一个全局共享的可学习的多项式系数构成的映射矩阵；
为了使得模型可以更高效地在 GPU 上运行，我们基于函数逼近理论用切比雪夫多项式来拟合卷积操作；因为，切比雪夫多项式的 n 阶基函数（n>1）都可以由 n-1 阶基函数和 n-2 阶基函数表示，所以函数滤波器的学习可以分解为一系列矩阵的迭代加法运算；

类型 说明 作用
卷积 加权求和  
膨胀卷积 每两列/行参数间有间隔 同样参数下具有大感受野，宜用于分割任务
反卷积
转置卷积		 补0（边界扩张，或均匀扩张-stride），然后旋转卷积核，再进行卷积  
形变卷积 多学习一个偏移层，参数位置可变化 使卷积聚焦于感兴趣物体，宜用于分割任务
     

上采样：双线性插值，unpooling，反卷积；

2 实验

2.1 鲁棒性

卷积核中的所有元素之间都是相关的，这使得卷积核更的方差更小、更光滑，最后获得对高斯噪声、旋转、平移和尺度变化更高的鲁棒性；详情参阅文献[13]；

2.2 消融实验

1) 基函数个数的影响
不同阶数的基函数去用来拟合不同复杂度的函数卷积核；
实验卷积核大小为 11*11，在结构感知卷积中基函数个数为 t={5,40,80,120,160}；当 t 为 5 的时候，结构感知卷积网络性能最差；随着 t 的增大，结构感知卷积网络的性能会优于传统卷积网络的性能，并且当 t>40 时已经有此优势了；这就意味着，传统的离散卷积核中的参数是有冗余的；也就是说，不仅仅高维的数据是嵌入在一个低维流形里面的，神经网络的海量参数也是嵌入在一个低维流形里面的（神经网络可以压缩的原因）；
2） 卷积网络的可迁移性
借助迁移，网络可以学习的更稳定、更快，并最终取得更好的性能；

3 应用

4 展望

  1. 理论研究
    • 模型压缩
    • 少样本学习
    • 持续学习:with a specific basis function
    • 深度学习过程解释
  2. 工程应用
    • 自动驾驶中雷达数据分类
    • 实时路径规划
    • 潜在用户挖掘(Amazon,Taobao,JD)

TOP

附录

A 推荐资料

[1]James Atwood and Don Towsley. Diffusion-convolutional neural networks. In NIPS,2016.
[2]Davide Boscaini, Jonathan Masci, Emanuele Rodolà, and M. M. Bronstein. Learningshape correspondence with anisotropic convolutional neural networks. In NIPS,2016.
[3]M. M. Bronstein, Joan Bruna, Yann LeCun, Arthur Szlam, and PierreVandergheynst. Geometric deep learning: Going beyond euclidean data. IEEESignal Process. Mag., 2017.
[4]Joan Bruna, Wojciech Zaremba, Arthur Szlam, and Yann LeCun. Spectral networksand locally connected networks on graphs. CoRR, 2013.
[5]Michael Defferrard, Xavier Bresson, and Pierre Vandergheynst. Convolutionalneural networks on graphs with fast localized spectral filtering. In NIPS,2016.
[6]Jianlong Chang, Jie Gu, Lingfeng Wang, Gaofeng Meng, Shiming Xiang, andChunhong Pan. Structure-Aware Convolutional Neural Networks. In NIPS 2018.
[7]T. N. Kipf and Max Welling. Semi-supervised classification with graphconvolutional networks. CoRR, 2016.
[8]Jonathan Masci, Davide Boscaini, M. M. Bronstein, and Pierre Vandergheynst.Geodesic convolutional neural networks on riemannian manifolds. In ICCVWorkshops, 2015.
[9]Federico Monti, Davide Boscaini, Jonathan Masci, Emanuele Rodolà, Jan Svoboda,and M. M. Bronstein. Geometric deep learning on graphs and manifolds usingmixture model cnns. In CVPR, 2017.
[10]Martin Simonovsky and Nikos Komodakis. Dynamic edge-conditioned filters inconvolutional neural networks on graphs. In CVPR, 2017.
[11]Nitika Verma, Edmond Boyer, and Jakob Verbeek. Dynamic filters in graphconvolutional networks. CoRR, 2017.
[12]Jifeng Dai, Haozhi Qi, Yuwen Xiong, Yi Li, Guodong Zhang, Han Hu, and YichenWei. Deformable convolutional networks. In ICCV, 2017
[13]Avraham Ruderman, N. C. Rabinowitz, A. S. Morcos, and Daniel Zoran. Learned deformation stability in convolutional neural networks. CoRR, abs/1804.04438,2018.

B 参考资料

  1. 常建龙. 深度卷积网络中的卷积算子研究进展[EB/OL]. https://mp.weixin.qq.com/s?__biz=MzIzNjc0MTMwMA==&mid=2247485700&idx=1&sn=4ca711a6292d5d97a6df392397f690ed&scene=21#wechat_redirect. 2018-10-22/2019-03-21.
  2. 各种卷积

Comments

You May Also Enjoy