「论文解读」 Weakly supervised 3D Reconstruction with Adversarial Constraint
论文发表时间:2017-05-31
作者: JunYoung Gwak, Christopher B. Choy, Animesh Garg, Manmohan Chandraker, Silvio Savarese
单位: 斯坦福
论文地址: https://arxiv.org/abs/1705.10904
官方代码: theano https://github.com/jgwak/McRecon
文章好难读哦
本篇论文骨骼清奇,核心用的 GAN 网络,但是通篇都不用 GAN 相关的术语,而且还解释了文章思路与 GAN 不同,问题是解释又很牵强:
| GAN 相关术语 | 本文的替换词汇(中) | 本文的替换词汇(中) |
|---|---|---|
| GAN | 基于对抗约束的弱监督重建 对抗优化 |
weakly supervised reconstruction with adversarial constraint constrained optimization |
| 对抗损失 | 惩罚函数 | penalty function |
| 判别器 | 流形约束 对抗约束 约束冲突 将生成结果约束到真实数据流形上 |
manifold constraint adversarial constraint constraint violation constrain the reconstruction to be in manifold of realistic shape |
| 数据分布 | 流形约束的边界 | barrier for manifold constraint |
| softmax | 对数界限 | log barrier |
是我没读懂还是论文太烂了
1 概述
GAN 实现三维重建;
2 方案
前导知识:深度学习基本知识,CNN,GAN, 3D
2.1 模型结构
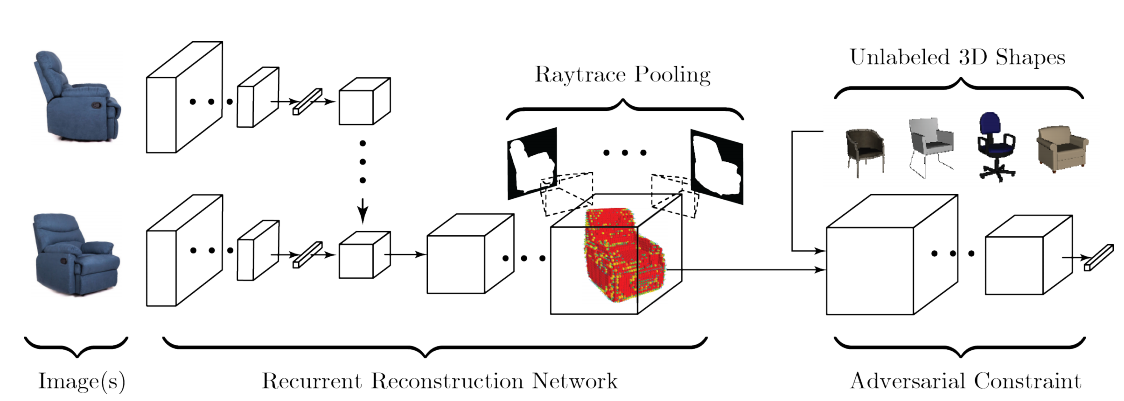
图1:网络结构
3 损失函数
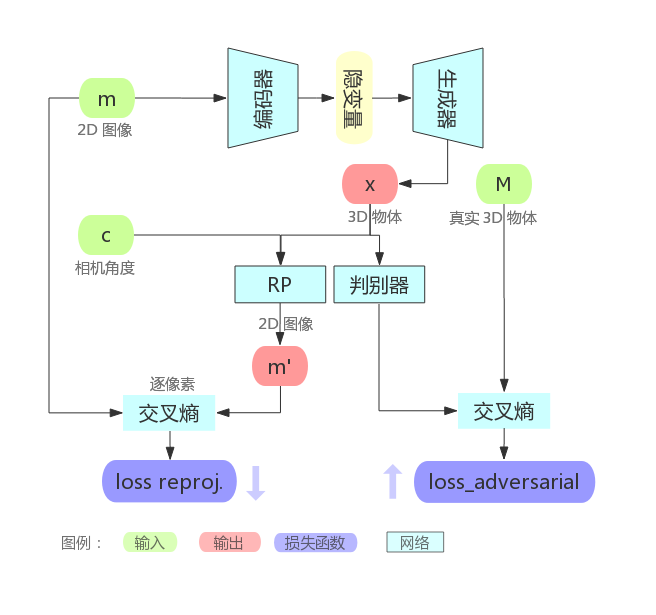
图2:网络简图
\(\begin{align}
\mathcal{L}_{reproj.}(x, \mathbf c, \mathbf m) &= {1 \over M} \sum_j^M \mathcal{L}_s(RP(x, c_j), m_j) \label{loss_project} \\
Loss &= \mathop{\mathbb{E}}\limits_{v \in views} [\mathcal{L}_{reproj.}(\hat x, m_v)] - {1 \over t} \log g(\hat x) \label{loss} \\
Loss_{discriminator} &= \mathop{\mathbb{E}}\limits_{x \sim p}[\log g(x)] + \mathop{\mathbb{E}}\limits_{x \sim q}[\log (1-g(x)] \label{Loss_discriminator} \\
\end{align}\)
公式 $\eqref{loss_project}$ 中 $M$ 是视图/角的个数,$c$ 是视角,$x$ 是生成的 3D 模型,$RP$ 是 3D 到 2D 的投影函数,$\mathcal{L}_s$ shi 逐像素的交叉熵;
公式 $\eqref{Loss_discriminator}$ 中 $p$ 是真实 3D 数据分布,$q$ 是生成的 3D 数据分布;
4 实验
4.1 数据集
ShapeNet,ObjectNet3D,OnlineProduct;
4.2 实验结果
现有方法的对比
评估矩阵
消融实验
ShapeNet
单视角真实数据训练
多视角真实数据训练
4.2.1 精度
4.2.2 速度
5 思考
1.什么是「流形」
manifold;
2.为什么文章中作者大量使用「把重建结果约束在真实 3D 物体的流形结构中」,而不是使用「3D 重建」
「3D 重建」这个概念并没有告诉我们使用的是无监督、弱监督还是监督,也就是范围太广;而「把重建结果约束在真实 3D 物体的流形结构中」很明显就是弱监督,而不是需要完整的 3D 标签来完成重建;
「把重建结果约束在真实 3D 物体的流形结构中」=「弱监督 3D 重建」=「把重建结果约束到真实的数据分布」=「GAN」;个人认为此处加入「流形」这个概念是为了提升论文的档次,并没有用「流形」这一特性来改进模型;
3.RayTrace 模块反向传播怎么做的
RayTrace 是将 3D 物体投影到 2D 上,投影过程使用了 MaxPooling 操作;所以,对 2D 的求导结果直接按 MaxPooling 的反向传播方式(拷贝梯度)传会 3D 即可;
1.判别器用的 softmax-crossentropy,这种方式效果真的好吗
6 总结
附录
A 术语
1. ill-posed problem
well posed problbem:解存在、唯一、稳定(输入连续变化时,输出不会跳变);
ill posed problem:「不适定问题」,也就是「不 well posed problem」,简单来说就是结果不唯一,比如 a+b=5,求 a 和 b 的值就是不适定问题;矩阵乘法如果是不适定问题,通常是因为那个矩阵不满秩,零空间不为空,这样即使真实解发生很大的变化,仍然得到相同的结果;所以对于不适定问题,需要做各种先验假设,来约束它,使它变为 well posed,从而能够求解;很多求逆的问题都是不适定问题;
在计算机视觉中,有很多任务不满足“适定”条件,通常不满足第二条和第三条;比如用GAN“伪造”图像的时候,这个任务就不满足“解的唯一性”;做图像超分辨率,或者对图像去雨去雾去模糊等等任务时,这些都没有一个标准答案,解有无数种;更重要的是,这些解都是不稳定的;
参考书:《逆问题数学理论导论》、《统计和计算中的逆问题》
图像处理中不适定问题(ill posed problem)或称为反问题(inverse Problem)
B 参考文献
- 光线追踪
- octree voxel-walking
Ray Tracing News. Linear-time Voxel Walking for Octrees, by Jim Arvo.
J. Arvo. Linear-time voxel walking for octrees. Ray Tracing News, 1(2), 1988. - raybox intersection algorithm
A. Williams, S. Barrus, R. K. Morley, and P. Shirley. An efficient and robust ray-box intersection algorithm. In ACM SIGGRAPH 2005 Courses, page 9. ACM, 2005.
- octree voxel-walking
Comments